Optimizations in different crypto libraries leads to weaker than expected keys; OpenSSL and gnuTLS generate slightly weaker keys than mbedTLS.
The "strength" of an RSA key against brute-force is related to how much of the P and Q the attacker knows / can eliminate. The more bits of the key the attacker knows, or the more of the relationship between P and Q, the weaker the key (I'm using imprecise terminology to make this easier to understand).
I'm using 512 bit keys in examples, because they are faster to generate than longer keys, but the principle is the same for all key lengths.
A 512 bit key has the msb (most significant bit) set. In order for this to be true, the MSB (most significant byte) of P and Q must both be >=128, so MSB(P)*MSB(Q)>= 32768 (e.g: 169*194 or 185*178). There are ~10,000 combinations that satisfy this, but Q > P, so we can ignore 1/2 of these, leaving only 5,000.
We also know that the lsb will be set - P and Q are prime, so P and Q are odd. Also, an odd number multiplied by an odd number is odd.
So, the 256bit primes are (ideally) 256 - 1 (lsb) - 1 (msb) - x. x is the small relationship between P and Q to satisfy MSB(P)*MSB(Q)>= 32768.
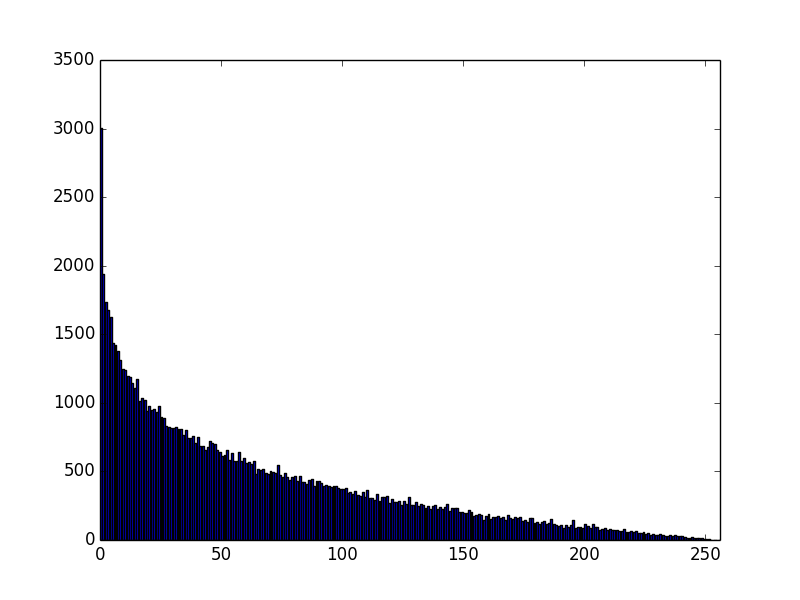
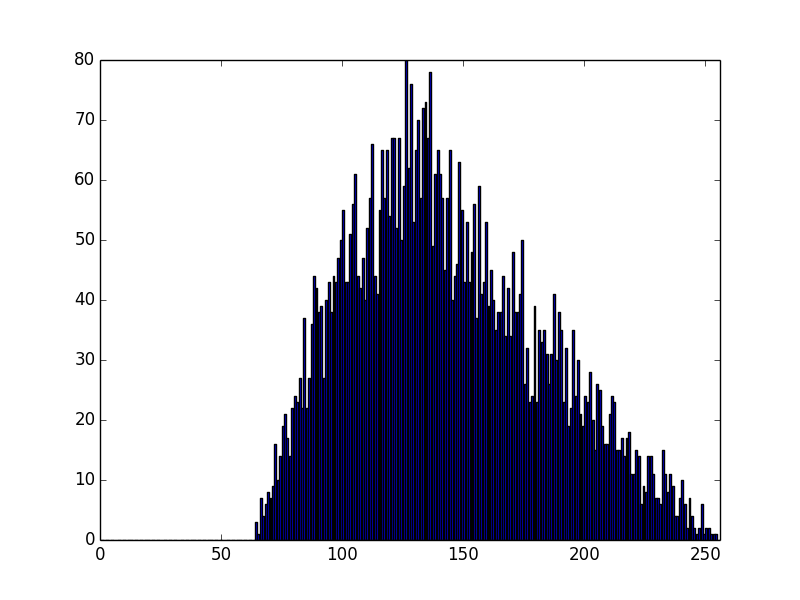
For some background, here is a graph of MSB(random(128, 255) * random (128, 255)). As you can see, nothing below 64 ((128 * 128) >> 8 == 64):
However, this doesn't satisfy the constraint that the msb must be 1. Let's plot this again, dropping all values where the high bit is not set (MSB(random(128, 255) * random (128, 255)>=128):
So, this is the distribution of MSB of moduli that satisfy the basic constraints that msb of MSB must be 1.
So, an attacker knows 3 things:
- the lsb of both P and Q is set (P and Q are prime)
- the msb of both P and Q is set, and
- there is some sort of minor relationship between P and Q (but this is no very helpful)
But, for all intents and purposes, a good key is 508 bits strong (2* (256 - 1 (lsb) - 1 (msb)).
Just for giggles (and because I have the script handy!), let's see what happens if we set the first *2* bits of P and Q high.
A plot of (random(128+64, 255) * random (128+64, 255):
Shifted more to the right (starts at 144), and steeper. Makes sense, (192*192) >> 8.
Great, now that we understand how things should look, let's look a the modulii from OpenSSL, gnuTLS and
mbedTLS.
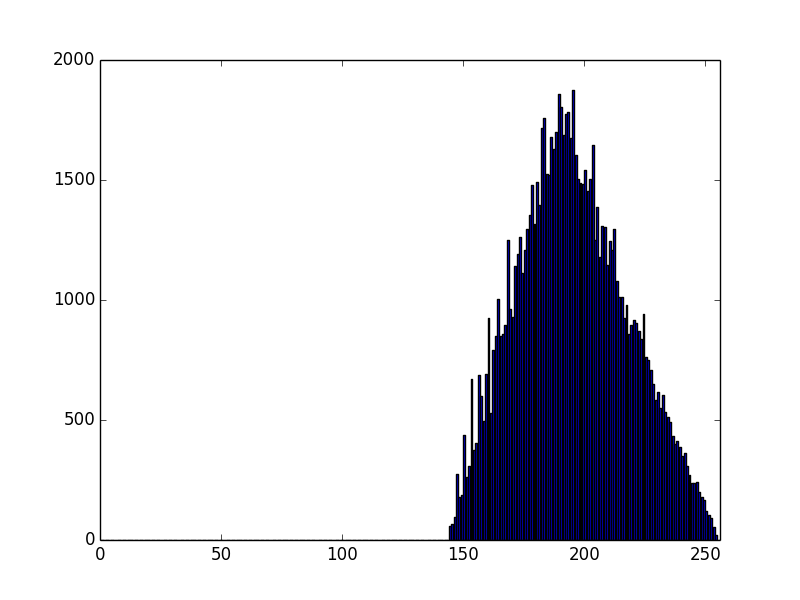
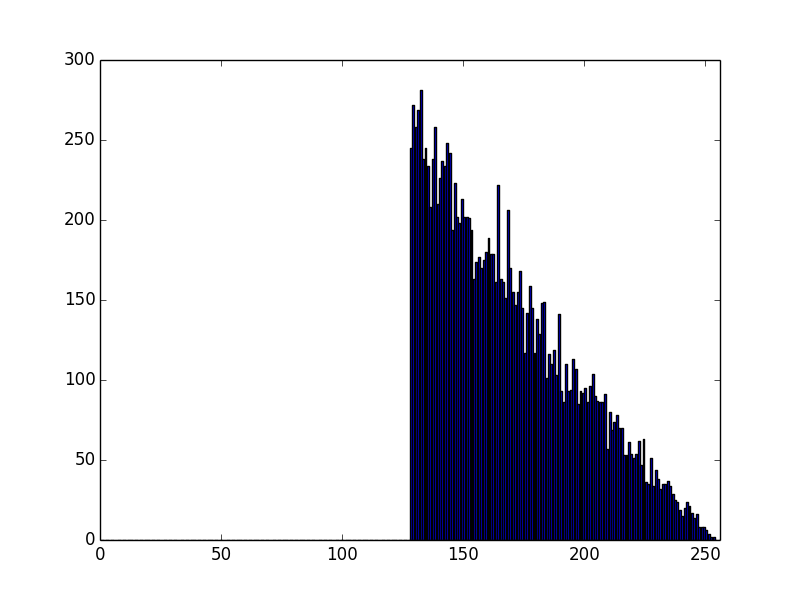
First, OpenSSL:
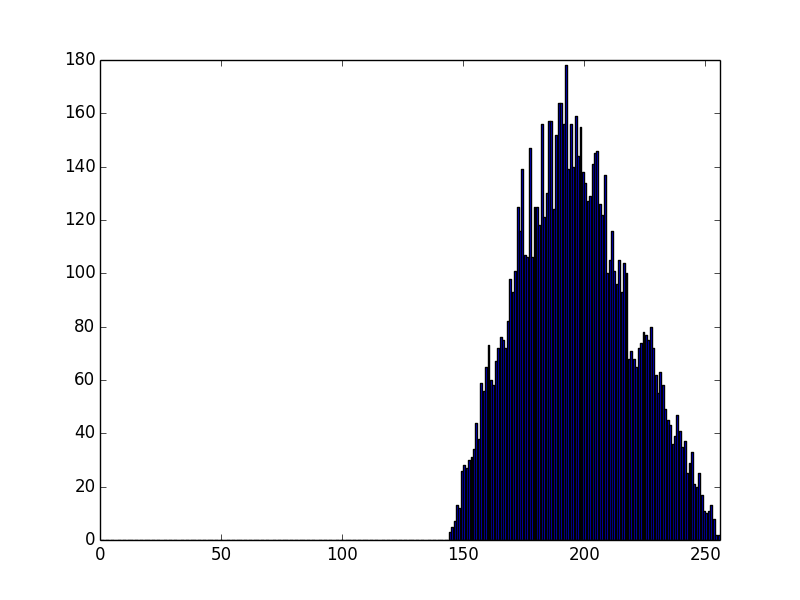
and GnuTLS:
So, gnuTLS (the low level crypto happens in nettle) and OpenSSL have identical distribution of their MSB of moduli, which seems to be the product of 2 numbers, with their 2 most significant bits set.
Let's check that -- we will graph the primes generated by them.
Errrrr... the lowest number is 192, which is 128 + 64....
That's suboptimal - the attacker now knows more about the primes than he should -- he knows that the first 2 bits are set in each, not just that the first bit is set.
Why is this?!
static int probable_prime(BIGNUM *rnd, int bits)
calls
BN_priv_rand(rnd, bits, BN_RAND_TOP_TWO, BN_RAND_BOTTOM_ODD)
What does BN_priv_rand called like this do?
"BN_rand() generates a cryptographically strong pseudo-random number of bits in length and stores it in rnd. If bits is less than zero, or too small to accommodate the requirements specified by the top and bottom parameters, an error is returned. The top parameters specifies requirements on the most significant bit of the generated number. If it is BN_RAND_TOP_ANY, there is no constraint. If it is BN_RAND_TOP_ONE, the top bit must be one. If it is BN_RAND_TOP_TWO, the two most significant bits of the number will be set to 1, so that the product of two such random numbers will always have 2*bits length. If bottom is BN_RAND_BOTTOM_ODD, the number will be odd; if it is BN_RAND_BOTTOM_ANY it can be odd or even. If bits is 1 then top cannot also be BN_RAND_FLG_TOPTWO."
Ah, so, BN_rand() will always return numbers with the 2 msb set, these get tested for primality, and then some pass, but they will always have the high two bits set.
At least I understand *why* now, but it seems like this creates a weakness in the generated keys - the attacker now knows 3 bits of the primes:
- the lsb is set
- the 2 msb are set.
This is more than just:
- the lsb is set
- the product of MSB(P, Q) >=32786 (5000 options)
I *think* that this means that the primes from OpenSSL / gnuTLS are only 253 bits, not 254, so the "512 bits" keys are 506bis, and not 508bit.
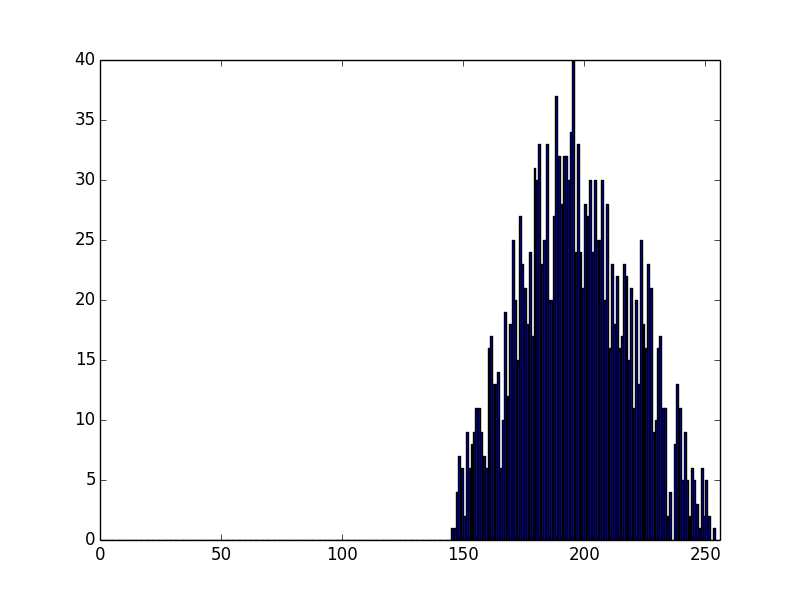
Anyway, let's looks at moduli from stock mbedTLS:
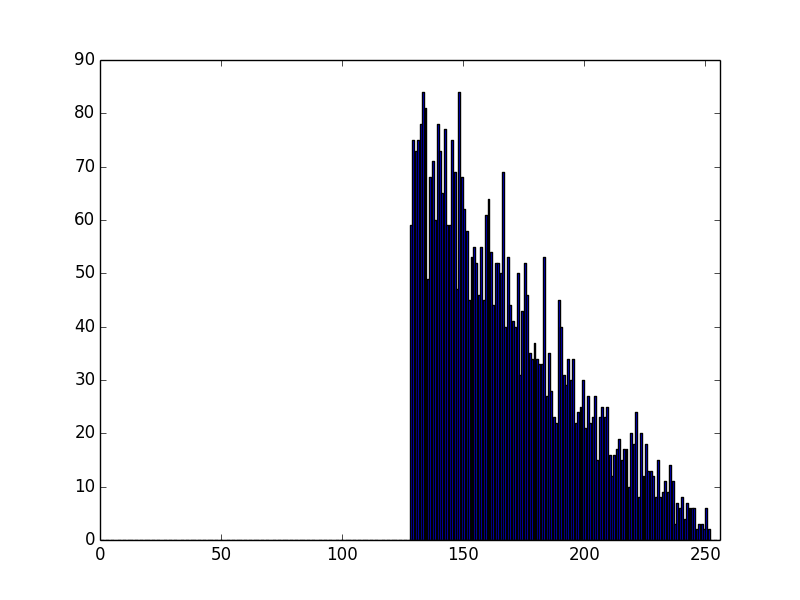
Well, that is noticeably different - and it looks like our ideal case.
Lets go look at the code. It seems like their distribution looks like like a product of 2 numbers, with only their high bits set, but they then ignore anything where the high bit is not set.
From: library/rsa.c
1: MBEDTLS_MPI_CHK( mbedtls_mpi_gen_prime( &ctx->P, ( nbits + 1 ) >> 1, 0,
2: f_rng, p_rng ) );
3:
4: MBEDTLS_MPI_CHK( mbedtls_mpi_gen_prime( &ctx->Q, ( nbits + 1 ) >> 1, 0,
5: f_rng, p_rng ) );
6:
7: if( mbedtls_mpi_cmp_mpi( &ctx->P, &ctx->Q ) < 0 )
8: mbedtls_mpi_swap( &ctx->P, &ctx->Q );
9:
10: if( mbedtls_mpi_cmp_mpi( &ctx->P, &ctx->Q ) == 0 )
11: continue;
12:
13: MBEDTLS_MPI_CHK( mbedtls_mpi_mul_mpi( &ctx->N, &ctx->P, &ctx->Q ) );
14: if( mbedtls_mpi_bitlen( &ctx->N ) != nbits )
15: continue;
Lines 1 - 5 make some primes.
Lines 7 - 8 sort them so Q>=P
Lines 10 - 11 makes sure P!=Q. I guess this doesn't hurt, but I'd expect a loud warning if they do - it would seem very likely that your random source is not random (unless, perhaps, you are making very small primes?).
Line 13 calculates the modulus.
Now for the "fun" bit...
Line 14-15 checks if the bitlength of the modulus != the requested keylength. Hmmm..
I threw in a debug statement, and sometimes the generated keylength is 1 less than the requested keylength.
Makes sense I guess - they don't set *2* high bits when calculating their primes, so sometimes you will get e.g (128 * 128) >>8 == 64. This is 0b0100 0000.
This does not have the highbit set, so it is (kinda) a 511 bit key.
Let's see what happens if we comment out that check:
Yup, now we are getting some moduli where the most significant byte is <128, and so the msb is not set. This means that the bitlength of the keys with this check removed is <512.
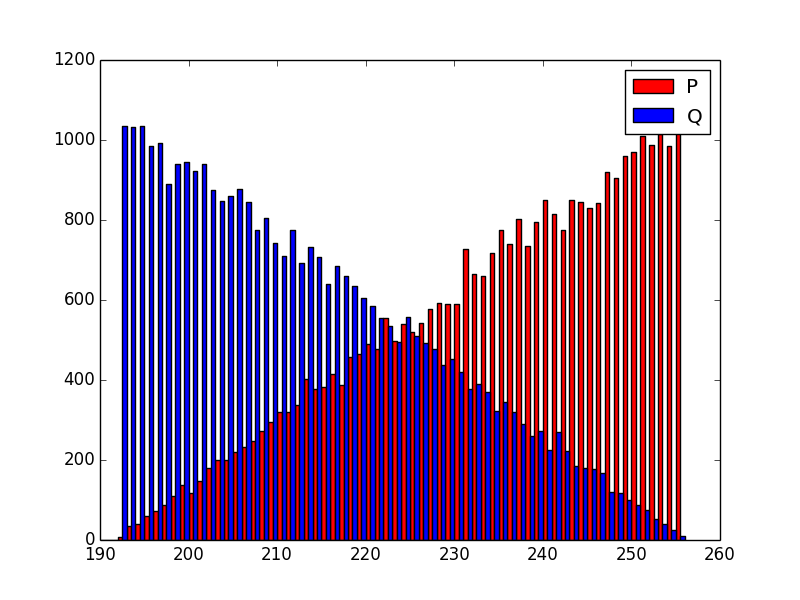
Ok, let's graph the primes from mbedTLS:
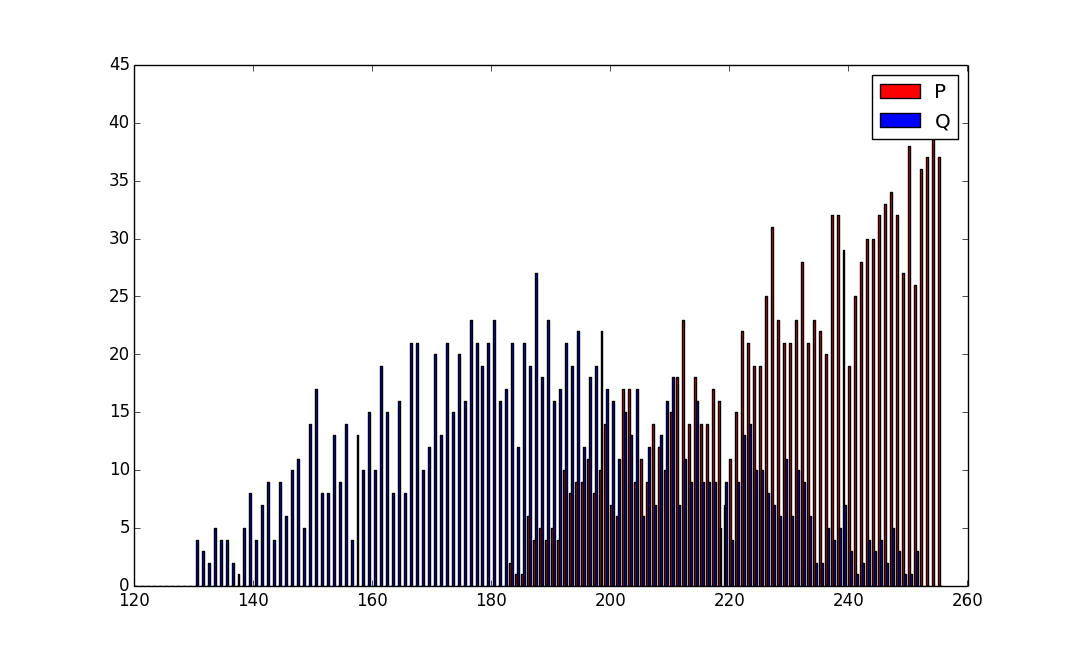
Looking closer, the lowest Q is 130 - this makes sense. (130 * 255) >>8 = 129.
So, it looks to me like mbedTLS makes stronger keys than OpenSSL / gnuTLS. There is not a *huge* difference (it's ~2bits (506 -> 508)), but it *is* noticeable, and it comes about from a (IMO) gratuitous optimization...